[알고리즘] 다익스트라 알고리즘
다익스트라(Dijkstra)는 최단 경로 탐색 문제에서 사용되는 알고리즘으로, 특정 노드에서 다른 노드로의 최소 비용을 찾아낼 때 사용하는 알고리즘이다.
알고리즘 분류는 탐욕(Greedy) 알고리즘이라고도 하며, 이미 탐색한 결과에 대해 계산하지 않고, 기존 결과를 재사용한다는 점에서 다이나믹 프로그래밍으로도 볼 수 있다.
노드의 방향이 양방향인지 단방향인지에 상관없이 문제에 적용할 수 있다.
흐름
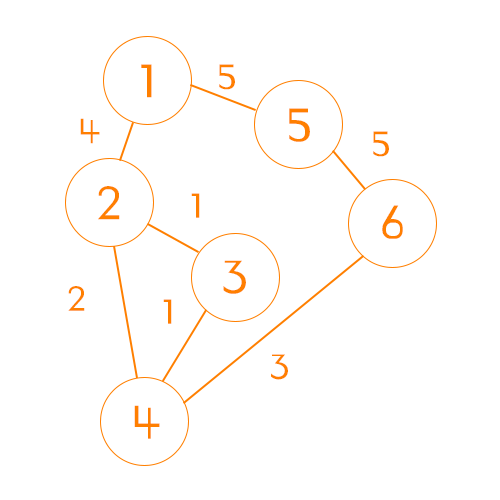
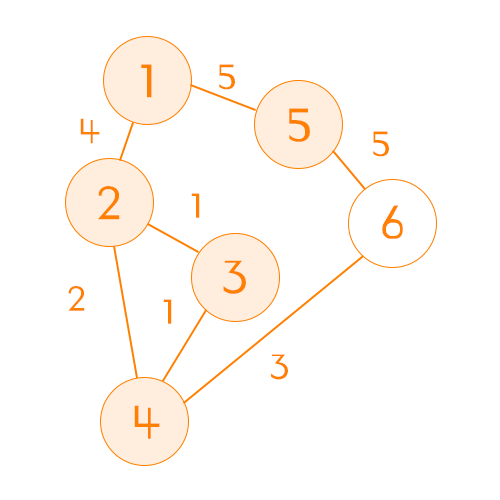
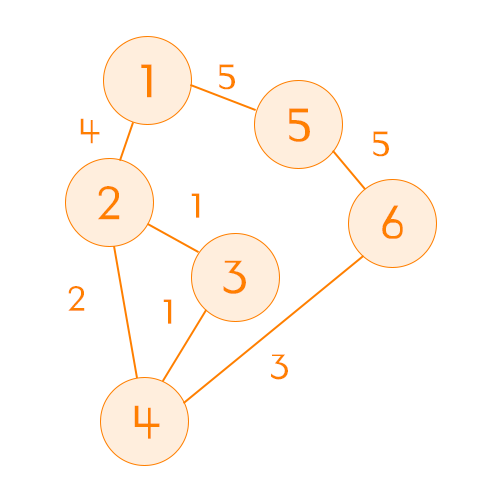
노드간 비용 초기화
위와 같은 그래프를 2차원 배열로 초기화 했을 때 아래와 같은 표가 그려진다.
| \ | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 비용 | 0 | 4 | INF | INF | 5 | INF |
| 2 | 4 | 0 | 1 | 2 | INF | INF |
| 3 | INF | 1 | 0 | 1 | INF | INF |
| 4 | INF | 2 | 1 | 0 | INF | 3 |
| 5 | 5 | INF | INF | INF | 0 | 5 |
| 6 | INF | INF | INF | 3 | 5 | 0 |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
private int[][] initializeGraph(int nodeCount, int[][] nodes) {
int nodesSize = nodes.length;
int[][] graph = new int[nodeCount + 1][nodeCount + 1];
for (int row = 1; row <= nodeCount; row++) {
for (int column = 1; column <= n; column++) {
// 같은 위치 비용 0 처리
if (row == column) {
graph[row][column] = 0; // 상수로 포장해 사용해주는 것이 좋다
}
// 방문 불가 처리
graph[row][column] = Integer.MAX_VALUE; // 상수로 포장해 사용해주는 것이 좋다
}
}
for (int nodeIndex = 1; nodeIndex <= nodesSize; nodeIndex++) {
int node1 = nodes[nodeIndex][0];
int node2 = nodes[nodeIndex][1];
int cost = nodes[nodeIndex][2];
graph[node1][node2] = cost;
graph[node2][node1] = cost;
}
return graph;
}
시작점 정하기
이제 시작점을 고르면 된다. 여기서는 시작 노드를 1로 하겠다. 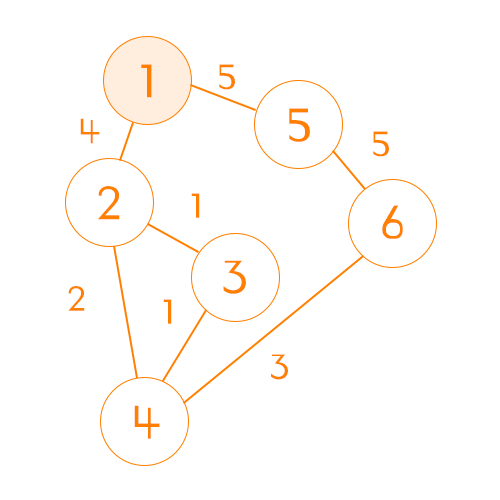
시작 노드를 정했다면 그래프에서 해당 시작점의 행을 가져오면 된다. | \ |1|2|3|4|5|6| |–|–|–|–|–|–|–| |비용|0|4|INF|INF|5|INF|
1
2
int[] distance = graph[1].clone();
boolean[] visited = new boolean[n];
비용이 작은 노드 부터 방문하기
| \ | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 업데이트 | 🌟 | 🌟 | ||||
| 비용 | 0 | 4 | INF | INF | 5 | INF |
| 방문여부 | ✅ | ❌ | ❌ | ❌ | ❌ | ❌ |
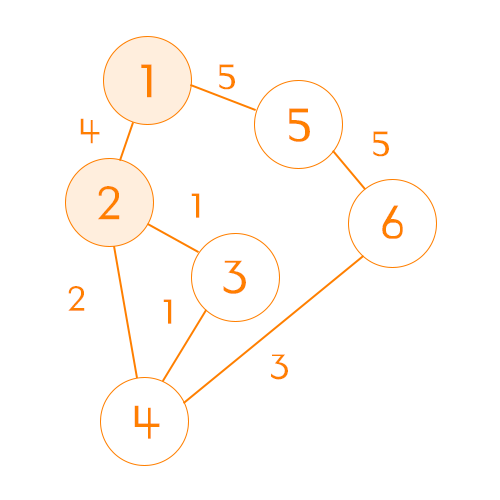
방문하지 않았으면서, 비용이 가장 작은 노드를 먼저 찾는다.
위 상황에서는 비용이 4인 2번 노드가 된다.
1번에서 찾은 노드의 다음 노드를 찾는다.
2번 노드의 다음 노드는 1, 3, 4번 노드이다.
방문했던 노드를 제외한 노드들의 비용과 현재 노드의 비용을 합한다.
2번 노드의 비용이 4이므로 3번 노드는 총 비용이 5 4번 노드는 총 비용이 6
시작 노드에서 해당 노드들의 방문 비용을 비교해서 업데이트 한다.
1번 노드에서 3번 노드로 가는 비용은 0으로 아직 방법이 없다. 1번 노드에서 4번 노드로 가는 비용은 0으로 아직 방법이 없다. 결론적으로 1번 노드에서 3번 노드와 4번노드를 가는 비용을 업데이트 한다.
| \ | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 업데이트 | 🌟 | 🌟 | ||||
| 비용 | 0 | 4 | 5 | 6 | 5 | INF |
| 방문여부 | ✅ | ✅ | ❌ | ❌ | ❌ | ❌ |
반복
모든 노드를 방문할 때까지 또는 원하는 노드를 방문할 때 까지 위 과정을 반복하면 된다. 여기서는 모든 노드의 경로를 찾을 때 까지 반복하겠다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
private int findMinNode(int n, int[] distance, boolean[] visited) {
int minNode = -1;
int minValue = Integer.MAX_VALUE;
for (int i = 1; i <= n; i++) {
if (visited[i] ||
distance[i] >= Integer.MAX_VALUE) {
continue;
}
minNode = i;
minValue = distance[i];
}
return minNode;
}
private void dijikstra(int n, int[][] graph) {
int[] distance = new int[nodeCount]; // 시작 지점의 다음 노드별 비용 리스트
int node = n;
boolean[] visited = new boolean[n + 1];
while (node > -1) {
visited[node] = true;
for (int nextNode = 1; nextNode <= nodeCount; nextNode++) {
int newDistance = distance[node] + graph[node][nextNode];
if (visited[nextNode] ||
distance[nextNode] <= newDistance) {
continue;
}
distance[nextNode] = newDistance;
}
node = findMinNode(n, distance, visited);
}
return distance;
}
| \ | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 업데이트 | ||||||
| 비용 | 0 | 4 | 5 | 6 | 5 | INF |
| 방문여부 | ✅ | ✅ | ✅ | ❌ | ❌ | ❌ |
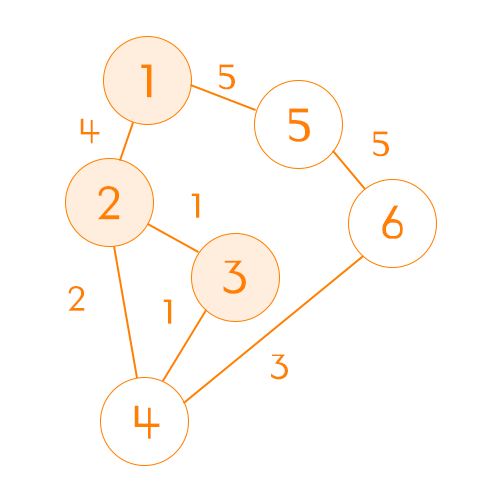
여기서 3번과 5번이 똑같이 5라는 비용인데 3번을 먼저 간 이유는 반복문을 통해 작은 수부터 검사했기 때문이다. 이 순서는 크게 중요하지 않다.
| \ | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 업데이트 | 🌟 | |||||
| 비용 | 0 | 4 | 5 | 6 | 5 | 10 |
| 방문여부 | ✅ | ✅ | ✅ | ❌ | ✅ | ❌ |
| \ | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 업데이트 | 🌟 | |||||
| 비용 | 0 | 4 | 5 | 6 | 5 | 9 |
| 방문여부 | ✅ | ✅ | ✅ | ✅ | ✅ | ❌ |
| \ | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 업데이트 | ||||||
| 비용 | 0 | 4 | 5 | 6 | 5 | 9 |
| 방문여부 | ✅ | ✅ | ✅ | ✅ | ✅ | ✅ |
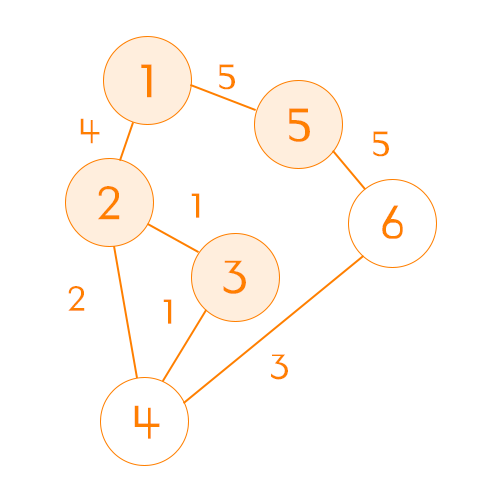
마지막 남은 한 개의 노드는 굳이 방문하지 않아도 된다. 마지막 노드에서 경유해서 갈 다른 노드는 이미 모두 방문했기 때문
여기서 궁금했던 점
나는 여기서 “이미 방문했던 노드의 비용을 업데이트하지 않아도 되는 것인가?” 라는 생각이 들었다. 하지만 다익스트라에선 가장 적은 비용의 노드부터 방문한다는 점에서 이러한 걱정을 할 필요가 없았다.
가령 1번 노드에서 2번 노드와 3번 노드를 갈 수 있다고 가정했을 때, 2번 노드에 가는 비용이 3이고, 3번 노드에 가는 비용이 4라고 하자. 3번 노드로 가는 경우 어떻게 해서도 2번 노드의 비용보다 적을 수 없다.
확장성
- distance 배열에서 가장 작은 값을 먼저 처리한다는 점에서 우선순위 큐(Priority Queue)를 적용하면 효율을 더 챙길 수 있을 것이다.
- for문으로 검사중인 노드의 다음 노드들을 확인하는데, 이때 for문으로 모든 노드를 확인하지 않고 Map이나 List를 사용하여 방문 가능한 노드들만 확인할 수 있다.
- 만약 node의 수가 많다면 int[][]와 같은 배열이 아닌 List를 사용해 메모리를 줄일 수 있다.
결론
기존의 DFS, BFS 방식으로 노드 문제를 많이 해결했었는데, 노드 문제들을 만날수록 고려해야하는 노드들이 많아지고, 시간을 초과하는 일이 빈번해지기에 다익스트라를 통해 이런 문제들을 해결할 수 있었다.
처음 다익스트라 알고리즘을 접했을 때는 정말 이렇게 풀면 효율적으로 풀 수 있는 건가? 생각했다. 실제로 코드를 작성하고, 노드의 흐름을 확인해봤을 때는 이해할 수 있었다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
public int getMinDistance(int start, int end, int nodeCount, int[][] nodes) {
int[][] graph = initializeGraph(nodeCount, nodes);
int[] distance = dijkstra(nodeCount, graph);
return distance[end];
}
private int[][] initializeGraph(int nodeCount, int[][] nodes) {
int nodesSize = nodes.length;
int[][] graph = new int[nodeCount + 1][nodeCount + 1];
for (int row = 1; row <= nodeCount; row++) {
for (int column = 1; column <= n; column++) {
// 같은 위치 비용 0 처리
if (row == column) {
graph[row][column] = 0; // 상수로 포장해 사용해주는 것이 좋다
}
// 방문 불가 처리
graph[row][column] = Integer.MAX_VALUE; // 상수로 포장해 사용해주는 것이 좋다
}
}
for (int nodeIndex = 1; nodeIndex <= nodesSize; nodeIndex++) {
int node1 = nodes[nodeIndex][0];
int node2 = nodes[nodeIndex][1];
int cost = nodes[nodeIndex][2];
graph[node1][node2] = cost;
graph[node2][node1] = cost;
}
return graph;
}
private int findMinNode(int nodeCount, int[] distance, boolean[] visited) {
int minNode = -1;
int minValue = Integer.MAX_VALUE;
for (int i = 1; i <= nodeCount; i++) {
if (visited[i] ||
distance[i] >= Integer.MAX_VALUE) {
continue;
}
minNode = i;
minValue = distance[i];
}
return minNode;
}
private void dijikstra(int start, int nodeCount, int[][] graph) {
int[] distance = new int[nodeCount]; // 시작 지점의 다음 노드별 비용 리스트
int node = nodeCount;
boolean[] visited = new boolean[nodeCount + 1];
while (node > -1) {
visited[node] = true;
for (int nextNode = 1; nextNode <= nodeCount; nextNode++) {
int newDistance = distance[node] + graph[node][nextNode];
if (visited[nextNode] ||
distance[nextNode] <= newDistance) {
continue;
}
distance[nextNode] = newDistance;
}
node = findMinNode(nodeCount, distance, visited);
}
return distance;
}