[알고리즘] 누적합 알고리즘
누적합(prefix sum) 알고리즘은 작거나, 큰 배열에서
부분적으로 배열의 값을 여러 번 업데이트 할 때 효율적으로 업데이트 할 수 있는 알고리즘이다.
업데이트 요청마다 반복문을 돌지 않고,
업데이트 정보를 저장해두었다가 한 번의 반복문으로 해결한다.
카카오에서 출제한 파괴되지 않은 건물을 예시로 알아보겠다.
흐름
흐름을 간단하게 설명한다면,
누적합 배열에 각 인덱스에 더할 값을 담은 후
마지막에 이 누적합 배열의 값을 원본 배열의 값과 합치는 방식이다.
- 누적합 배열에 업데이트 정보 저장
- 반복문으로 인덱스별 최종 업데이트 값 저장
- 누적합 배열의 값을 원본 배열에 합산
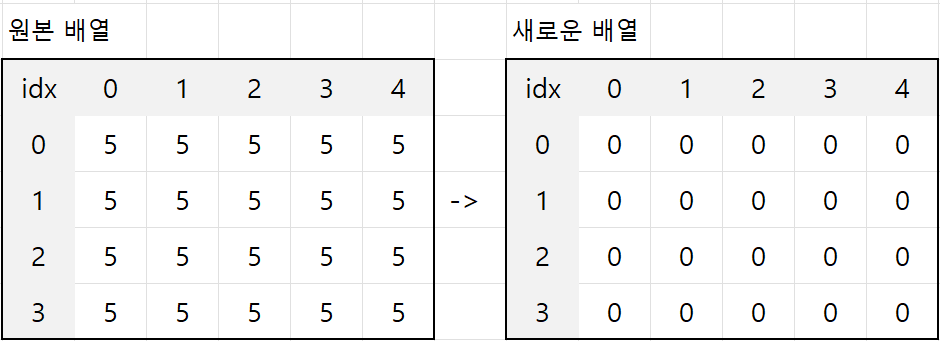
1. 새로운 배열 선언
원본 배열과 동일한 크기의 배열을 만든다.
그리고 해당 배열을 모두 0으로 초기화한다.
이 새로운 배열을 누적합 배열이라고 하겠다.
2. 업데이트 정보를 담은 배열을 누적합 배열에 적용하기
업데이트 배열 설명
아래는 업데이트 정보를 담은 배열이다.
각 배열의 인덱스별 의미는 아래와 같다.
| 인덱스 | 의미 | 설명 |
|---|---|---|
| 0 | type | 1일 때 degree를 뺀다. 2일 때 degree를 더한다. |
| 1 | row1 | 첫 번째 행을 의미한다. |
| 2 | col1 | 첫 번째 열을 의미한다. |
| 3 | row2 | 두 번째 행을 의미한다. |
| 4 | col1 | 두 번째 열을 의미한다. |
| 5 | degree | 연산할 값이다. |
1
2
3
4
5
6
7
8
// [0,1]은 [row,col]를 의미
[
[1, 0, 0, 3, 4, 4], // [0,0] ~ [3,4] 영역에 4를 뺀다는 의미.
[1, 2, 0, 2, 3, 2], // [2,0] ~ [2,3] 영역에 2를 뺀다는 의미.
[2, 1, 0, 3, 1, 2], // [1,0] ~ [3,1] 영역에 2를 더한다는 의미.
[1, 0, 1, 3, 3, 1] // [0,1] ~ [3,3] 영역에 1을 뺀다는 의미.
];
배열 업데이트
누적합에서 가장 중요한 부분이다.
어떻게 반복문을 사용하지 않고 영역을 업데이트할 것인가에 대한 내용이다.
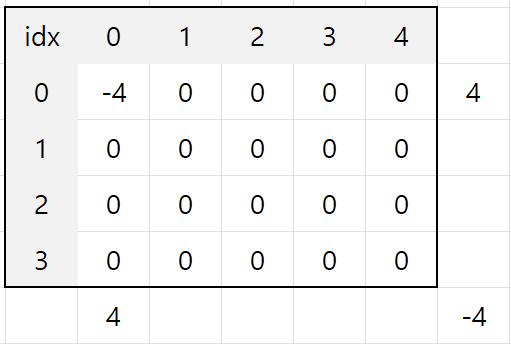
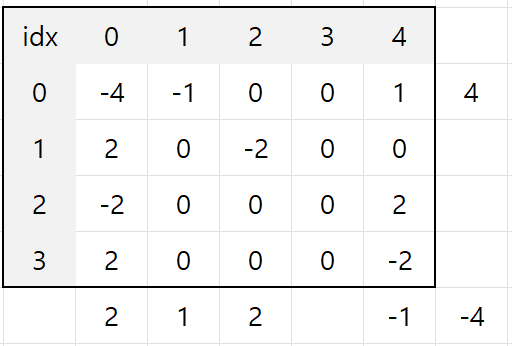
먼저 누적합 배열에서 업데이트할 영역의 가장 좌측 상단의 인덱스에 업데이트 할 값을 넣는다.
[1, 0, 0, 3, 4, 4] 이 업데이트 정보를 예시로, [0, 0]에 -4를 넣게된다.
이렇게 업데이트 영역 좌측 상단에 업데이트할 값을 넣어주는 이유는,
최종 단계에서 이 값이 반복문을 돌면서
인덱스가 왼쪽의 값 + 위의 값 - 왼쪽 상단(대각선)의 값을 가지기 떄문이다.
1
2
[r,c] += [r, c - 1] + [r - 1,c];
[r,c] -= [r - 1, c + 1];
이렇게 업데이트 영역의 시작 인덱스에 값을 넣어줬다.
여기서 끝이 아니고, 업데이트 영역 바깥쪽에서 해당 업데이트 값이 적용되지 않도록 해주어야 한다.
아까 설명한 것 처럼 누적합은 최후에 반복문을 통해 주변 값을 합산하는 구조이다.
그렇기 떄문에 그대로 사용하면 4번열 이후 및 3번 행 이후에도 -4라는 값이 입력되게 된다.
4번 열 이후부터는
-4가 적용되지 않아야 하며,
3번 행 이후부터도-4가 적용되지 않아야 한다.
그러기 위해서는 아래와 같이 -4를 0으로 만들어줄 4를 해당 인덱스에 입력해주면 된다.
그렇게 되면 한 행씩 계산했을 때 [0, 1] += [0, 0] + [-1, 0] - [-1, -1]이 된다.
이를 변환하면 0 += -4 + 0 - 0인 -4가 된다.
-1과 같이 불가능한 인덱스는 0으로 처리한다.
그랬을 때, 첫 번째 행은 -4가 되고,
두 번째 행 [1, 0]은 0 += 0 + (-4) - 0이 된다.
계속한다면 3번행까지 전부 -4가 된다.
이렇게 영역 안쪽은 문제 없이 잘 되는 것을 알 수 있다.
하지만 영역 바깥이라면?
우리가 4를 우측과 하단에 추가해줘서 [4, 0]을 기준으로 설명하자면,
4 += 0 + (-4) - 0이 된다. 결론적으로 0이되면서 영역 밖에는 적용되지 않는 것을 알 수 있다.
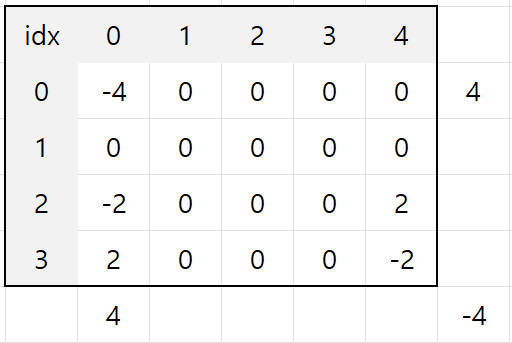
그런데 사진을 보면 영역 밖 대각선 아래에 -4가 또 나와있다. 왜 그럴까?
그 이유는 아래쪽이나 오른쪽의 바깥 영역쪽은 합산 과정에서 업데이트 영역이 있지만,
대각에 위치한 인덱스는 위쪽, 왼쪽에 업데이트 영역에 대한 값이 적용되어있지 않기 때문이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 하단은 위쪽에 업데이트 값이 존재함
-4 -4 -4 -4
4 0 0 0
// 우측은 왼쪽에 업데이트 값이 존재함
-4 4
-4 0
-4 0
-4 0
// 대각은 위쪽, 왼쪽 모두 업데이트 값이 존재하지 않음
-4 0
0 -4
이게 무슨 원리인가?
가능한 적은 접근으로 누적합을 만든다고 생각해보면 이해하기 쉬울 것이다.
만약 인덱스가 위쪽 값이 아닌 왼쪽 값만을 합산한다고 생각해보자.
업데이트 영역의 모든 행에 -4를 넣어주어야 한다.
또한 업데이트 영역이 끝나는 지점의 영역의 모든 행에도 4를 넣어주어야 한다.
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| -4 | 0 | 0 | 0 | 0 | 4 |
| -4 | 0 | 0 | 0 | 0 | 4 |
| -4 | 0 | 0 | 0 | 0 | 4 |
반대로 위쪽 인덱스의 값만을 합산한다고 생각해도 마찬가지이다.
더 적은 접근을 위해 왼쪽 및 오른쪽의 값을 합산하려고 하고 있다.
그러면 왼쪽 위 인덱스를 빼주는 이유는 무엇인가?
우선은 위쪽 인덱스와 왼쪽 인덱스 값을 합산한다는 점에서
둘이 같은 값을 가지는 경우가 있다.
| 0 | 1 |
|---|---|
| -4 | -4 |
| -4 | 0 |
이런 중복 합산을 방지해주기 위해 왼쪽 대각선을 빼주는 원리이다.
어떻게 동작하는 것인가?
이따 최종적으로 연산을 한 번 더 하겠지만, 간단히 설명하자면
[0][0] 부터 위의 값과 좌측의 값을 더하고, 대각선 좌측 위의 값을 빼보자.
그렇다면 아래와 같은 배열이 나오게 된다. 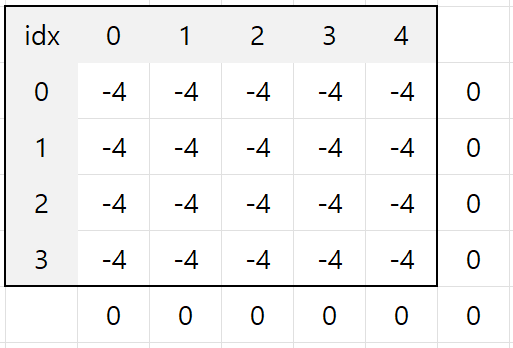
아마 위 사진을 보고 다시 위 글을 읽으면 바로 이해할 것이라고 생각한다.
물론 배열 밖의 값들은 실제로 배열에 적용되지 않지만, 설명을 위해 넣었다.
정확히 우리가 빼고자 했던 [0][0] 부터 [3][4] 까지 -4로 적용했다.
또한 그 바깥은 0으로 다시 돌아온다.
자세한 설명은 계속해서 보자.
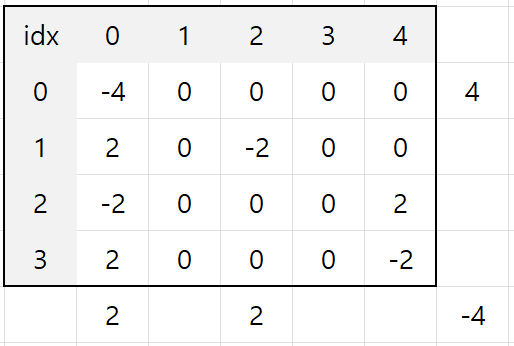
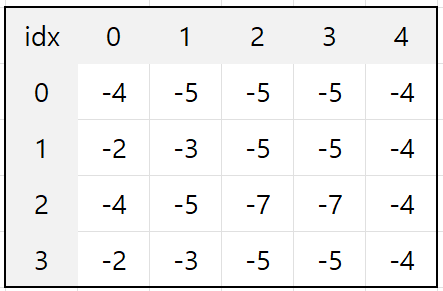
2번째 배열 업데이트
[1,2,0,2,3,2]
3번째 배열 업데이트
[2,1,0,3,1,2]
4번째 배열 업데이트
[1,0,1,3,3,1]
부분합 계산
드디어 모든 부분 배열에 대한 업데이트 배열을 만들게 되었다.
이제 첫 번째 배열 업데이트 때 했던 계산을 해보자.
[0][0]부터 배열의 끝([3][4])까지 아래 연산을 진행할 것이다.
1
arr[r][c] += arr[r - 1][c] + arr[r][c - 1] - arr[r - 1][c - 1]
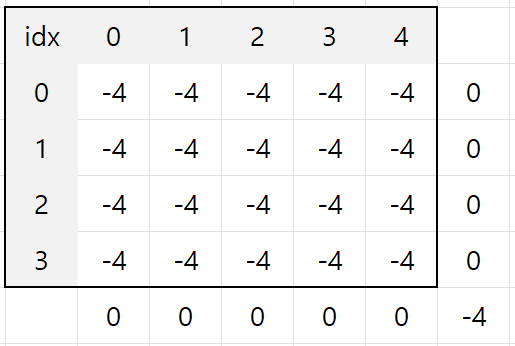
그렇다면 아래와 같은 결과가 나오게 된다.
원본 배열과 합
본 문제에서는 결과 값이 0보다 큰 인덱스의 수만 알아내면 되기 때문에 직접 배열에 더하진 않았다.
각 문제에 맞게 적용해서 사용하자.
최종 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
import java.util.Arrays;
class Solution {
private static final Integer TYPE_INDEX = 0;
private static final Integer R1_INDEX = 1;
private static final Integer C1_INDEX = 2;
private static final Integer R2_INDEX = 3;
private static final Integer C2_INDEX = 4;
private static final Integer DEGREE_INDEX = 5;
public int solution(int[][] board, int[][] skill) {
int boardHeight = board.length;
int boardWidth = board[0].length;
int[][] prefixSumArray = getPrefixArray(boardHeight, boardWidth, skill);
calculatePrefixSum(boardHeight, boardWidth, prefixSumArray);
int answer = 0;
for (int row = 0; row < boardHeight; row++) {
for (int col = 0; col < boardWidth; col++) {
if (prefixSumArray[row][col] + board[row][col] > 0) {
answer++;
}
}
}
return answer;
}
private void calculatePrefixSum(int height, int width, int[][] prefix) {
for (int row = 0; row <= height; row++) {
for (int col = 0; col <= width; col++) {
int a = 0;
int b = 0;
int c = 0;
if (row - 1 >= 0) {
a = prefix[row - 1][col];
}
if (col - 1 >= 0) {
b = prefix[row][col - 1];
}
if (row - 1 >= 0 && col - 1 >= 0) {
c = prefix[row - 1][col - 1];
}
prefix[row][col] += a + b - c;
}
}
}
private int[][] getPrefixArray(int height, int width, int[][] skill) {
int[][] prefixSumArray = new int[height + 1][width + 1];
int type, r1, c1, r2, c2, degree;
for (int[] eachSkill : skill) {
type = eachSkill[TYPE_INDEX];
r1 = eachSkill[R1_INDEX];
c1 = eachSkill[C1_INDEX];
r2 = eachSkill[R2_INDEX];
c2 = eachSkill[C2_INDEX];
degree = eachSkill[DEGREE_INDEX];
if (eachSkill[0] == 1) {
degree *= -1;
}
prefixSumArray[r1][c1] += degree;
prefixSumArray[r2 + 1][c1] -= degree;
prefixSumArray[r1][c2 + 1] -= degree;
prefixSumArray[r2 + 1][c2 + 1] += degree;
}
return prefixSumArray;
}
}
결론
처음에는 다른 블로그에서 설명해준 누적합을 통해 학습했다.
그 블로그들에서는 행 계산 따로, 열 계산 따로 하는 코드로 확인했다.
하지만 더 줄일 수 있을 것 같아 알아본 결과… 한 번에 할 수 있었다.
하지만 이로 인해 궁금증이 생겼었다.
어떻게해서 앞에서와 같은 식이 적용되는 것일까?
1
arr[r][c] += arr[r - 1][c] + arr[r][c - 1] - arr[r - 1][c - 1]
물론 앞에서도 설명했다. 하지만 조금더 길게 설명해보고자 한다.
우리는 arr[r1][c1]에 연산 해야 할 값을 넣었고, arr[r2 + 1][c1] 과 arr[r1][c2 + 1] 에 값에 -1을 곱한 값을 넣었다.
이 행동의 의미는 “해당 위치를 넘어갔을 때 다시 0으로 돌아와라” 라는 것을 의미한다.
즉, 범위를 넘어갔을 때 아무 값도 계산하지 않도록 바깥 범위에 반대의 값(* -1)을 넣은 것이다.
최종적으로 arr[r2 + 1][c2 + 1]을 들어왔을 때 바로 위와 왼쪽인 arr[r2 + 1][c2]와 arr[r2][c2 + 1]는 확실하게 0이고, arr[r2][c2]는 확실하게 -4기 때문에 0 + 0 - (-4) + ?와 같은 식에서 ?가 - (-4)와 반대인 -4가 들어가야했던 것이다.
결론은 이러한 부분 업데이트 방식은 우리가 원하는 부분만 정확히 수정하지만, 더 효율적으로 수정하는 좋은 알고리즘이라고 볼 수 있다. 처음 이 알고리즘 문제를 마주했을 때, 어떻게 풀지 막막했다. 풀이법을 알아내고 생각보다 쉬워 많이 당황했다…